Understanding and working with the square root of 2 is critical to solving algebra and geometry problems. While you can always use a scientific calculator to do it, learning how to calculate the square root of 2 by hand can help when you don’t have one.
In this post, we will go over the origins, proof of irrationality, and different methods of calculating the square root of 2 with examples.
Understanding the Square Root of 2
The first recorded history of the number goes back to Babylon, where tablet YBC 7289 was found. Scientists approximate the tablet to date back to between 1800 B.C. and 1600 B.C.; however, its mathematical significance was not recognized till 1945.
What is Square Root of 2?
In the simplest terms, the square root is the inverse operation of squaring. The square root of any number x is represented as √x, and multiplying √x with itself gives us x.
Since we’re discussing the square root of 2, let’s replace x with 2. Finding √2 answers the question, “what number should be multiplied with itself to be equal to 2?”
The square root of 4 equals 2. But the square root of 2 is not a regular integer; it is irrational.
The Greeks proved that the diagonal length of a square whose sides are one unit long could not be rational.
The proof of the existence of irrational numbers is attributed to the Greek philosopher Pythagoras, who found that numbers can never be written in the form of pq where p and q are integers and q is not zero. In addition, the existence of √2 is proved by the Pythagorean Theorem.
—
Fact: International paper sizes (A0, A1, A2,…) are based on √2. It is how the papers maintain proportion across sizes.
—
Proving the Irrationality of the Square Root of 2
The proof elucidated below is one of the classic proofs by contradiction. The idea with these proofs is that we want to show that some statement Z is true, so we assume that it’s not true and find a contradiction. And since there are no contradictions in math, statement Z has to be true.
Let’s assume that √2 is rational. In other words, it can be expressed as p/q, where p and q do not share common factors. Writing this as an equation:
√2 = p/q
Squaring the equation on both sides:
2 = p² / q²
Which implies:
p² = 2q²
The above equation indicates that p² is even, which can only be true if p is even. However, if p is even, it will also mean that p² is divisible by 4.
By the same logic, q² and q are also even. We assumed that p and q do not have common factors, but following these steps proves that they have common factors.
This contradiction proves that √2 cannot be rational. But it happens to be a very useful number in algebra and geometry.
While mathematicians have calculated the value of √2 up to ten trillion decimal places, the actual value of the number remains undetermined.
Finding the Square Root of 2
You can calculate the square root of 2 using these simple methods:
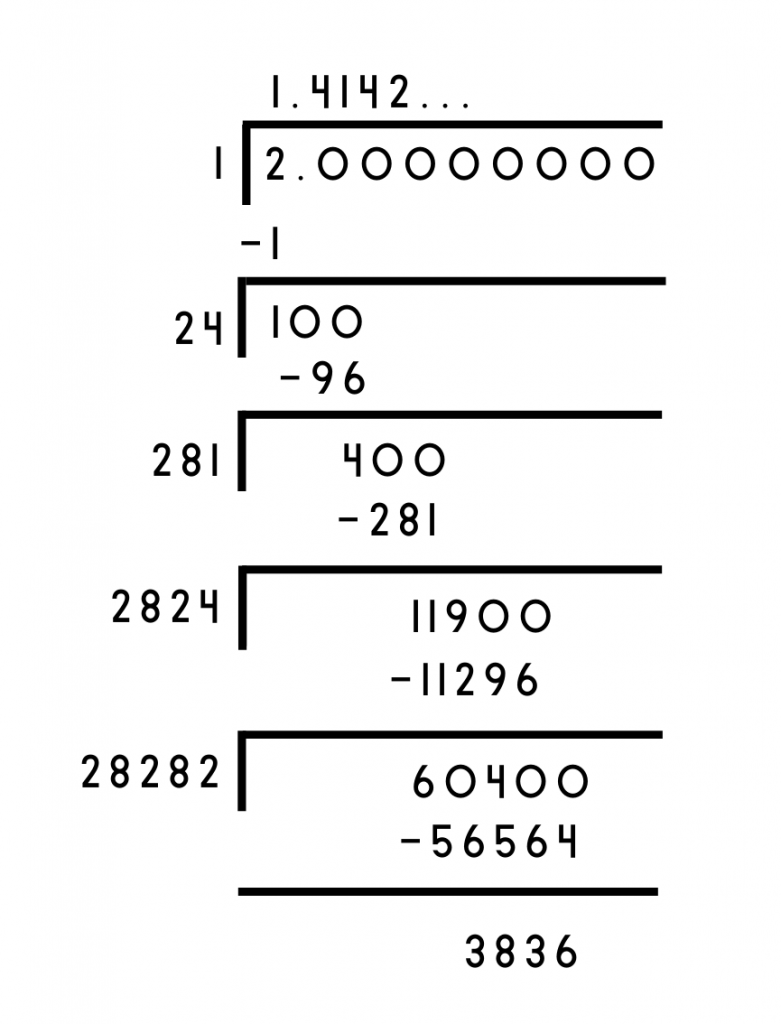
Long Division Method
Finding rational approximations of square roots like √2, √3, √5 can seem difficult since they are not perfect squares. But the long division method makes calculating irrational numbers like √2 uncomplicated. Here’s how you do it:
- First, find the largest number whose square is less than or equal to 2. Use it as a divisor and write the remainder.
- Place a point after the first digit in the quotient to indicate decimals.
- Bring down two zeros to the remainder to make the dividend 100.
- Now, guess the largest possible digit such that when the new divisor is multiplied with it, the product is less than or equal to the dividend.
- Carry out the division to work out the remainder.
- Repeat the process from step 4 to calculate √2 to the decimal places you want.
Estimation and Approximation Method
The estimation and approximation method involves using the formula y = √x. It can be rewritten as:
((x/y)+y)
2
This gives us the iteration formula:
Yn+1 = ((x/Yn)+Yn)
2
Iterating through the formula:
Iteration 1:
y1 = 2 + 1 = 1.5
2
Iteration 2:
y1 = 4/3 + (3/2) = 1.4166
2
Iteration 3:
y1 = 24/17 + (17/12) = 1.414215
2
The more you iterate, the closer the value gets to √2.
—
Note: √2 can also be expressed as a continued fraction
1 + 1
2+ 1
2+ 1
2+…
which is shortened to [1;2,2,2,…].
—
You can find the square root of any number on any device with an internet connection using the Meta-Calculator Root Calculator. All you have to do is enter the number and hit “Calculate.”
Examples of Square Root of 2
1. Find the length of the diagonal of a square made from four unit squares
The length of the diagonal of a square of side length 1 is √2. Since the square is made of four unit squares, the diagonal will be the length of the sum of the diagonal lengths of two unit squares.
Hence the length of the diagonal is 2√2.
2. What is the diagonal’s length in a square if its sides are two units long?
Applying the Pythagorean Theorem, the diagonal of the square is equal to √2 * (length of side). Hence the diagonal is 2.828 units long.

