Whether you want to verify your answer or skip calculating limits entirely, a calculator will help you. But there’s more that calculators can do for you.
Some limits problems cannot be solved algebraically, but a calculator can solve these problems.
Working with limits on a calculator is a little complicated. There are no buttons that you can press to feed in the limits of your functions directly into the calculator. So, working out the limit of a function with a calculator will require you to learn to use specific functions on the calculator.
In this post, we highlight the different techniques you can use to access a scientific calculator’s limit-finding functionalities.
What are Limits?
Limits are the foundation of all of calculus. They are what allow us to make sense of derivatives, integrals, and continuity. What’s more relevant is that limits allow us to analyze the behavior of functions at different points.
Finding the limit of a function (let’s say, function f(x)) will define its behavior when it’s near the “x” value. But it’s important to note that finding this value does not inherently provide the value of the function at “x.”
f(x) = L
The equation above can be read as the limit of f(x) as x approaches c is equal to L.
How to Calculate Limit with A Calculator
There are three ways of calculating limits with a calculator.
Method #1: Plugging in Numbers Close to the Arrow Number
Let’s say we have to test the following limit function:
x 2 -25
x-5
Now, to test this limit function, plug in the numbers that are slightly lower and slightly higher than the arrow number into the function.
To do this, turn on your calculator, and type in the first number that you want to use in the equation. Continuing with the example above, the first number will be 4.9999.
Next, press the “Sto” button, which is the store button, and then press the “x” button. Doing this will store the value 4.
9999 into “x.”
Now, you must type in the function into the calculator. Since the value you want substituted is stored in memory, the result will appear when you hit the enter key.
You will notice that the result for this example is 9.9999, which is extremely close to the round number 10. With this, we can conclude that the answer is likely 10.
The next step is to test the function from the other side by plugging in or substituting a number that’s greater than 5. Let’s take 5.0001 and go through the process again.
Type in 5.0001 in the calculator, hit “Sto,” and then enter the function 
into the calculator. Hit the enter button on the calculator.
The answer you see should be 10.0001, which is extremely close to the round number 10. This makes it almost certain that the answer we’re looking for is 10.
We’ve explained this method using the TI-84 scientific calculator. However, you will get the same result if you use the same technique with another calculator.
Method #2: Evaluating Limits Using Tables
To use this method, you will need a calculator with a graphing function. Most new scientific calculators come with this function built-in.
Turn on your calculator and switch to its graphing mode. Next, you must enter the equation that you want to find the limit of.
Let’s use the same example as before and enter y = into the calculator. Next, navigate to the “table set up” menu and enter the arrow number, which in this case is 5, as the table start number.
Then enter a small number like 0.001 as the ∆Tbl value. The ∆Tbl value defines the size of the increments of “x” in the table.
Now, when you press the “Table” button, the table will appear. Scroll along the results and find a few numbers less than five. You will see a table similar to the one below:
| x | y |
| 4.998 | 9.998 |
| 4.999 | 9.999 |
| 5 | Error |
| 5.001 | 10.001 |
| 5.002 | 10.002 |
| 5.003 | 10.003 |
You will see that the value of y gets close to 10 as the x value closes in on 5 from both above and below. From this, we can almost certainly conclude that 10 is the limit.
Method #3: Estimating a Limit Using Graphing Function
Let’s explain this approach by finding the limit of the function
x 2 – 9
x + 3
Now, in this method, instead of letting the table do the work, we will type in the values closest to -3 into the calculator.
Grab a piece of paper and a pen, and make a table with values close to -3, like so:
| x | y |
| -3.1 | |
| -3.01 | |
| -3.001 | |
| -3 | |
| -2.999 | |
| -2.99 | |
| -2.9 |
Now that you have a table ready to note the values down press the “Y=” button on your calculator. A screen with Y1, Y2, Y3, and so on will appear.
Navigate your cursor to Y1 and feed the function into it. You can then press the graph button on the calculator, which will then instruct the calculator to draw a graph of the function.
In this example, the graph should draw a straight, diagonal line.
To insert “x” values into the graph and find the corresponding “y” values, you will need to use the “Calc” function on the calculator. On the TI-84 Plus, press the “2ND” and then the “Trace” button to access this feature.
A menu with the title “CALCULATE” should appear.
We need to use the first option, “value,” which is automatically highlighted when the menu appears. So, you can press the enter key on the calculator directly.
An “X=” will appear under the graph. Now, you can enter the values of “x” you want to plug into the function.
Entering -3.1 and pressing the enter key will give you a result of -6.1. You can note this down in the table.
To enter the next value into the equation, you must go to the “CALCULATE” menu again and select the value option.
After you find all of the values, your table should look like this:
| x | y |
| -3.1 | -6.1 |
| -3.01 | -6.01 |
| -3.001 | -6.001 |
| -3 | |
| -2.999 | -5.999 |
| -2.99 | -5.99 |
| -2.9 | -5.9 |
From the data above, we can infer that as the x value comes close to -3, the y value approaches -6. This is a good enough estimate of the limit of the function.
Here is a video tutorial you can follow to use this method of calculating the limits of functions.
Limitations of Solving Limits with Calculators
Using the methods above to evaluate the limits of functions is useful for several reasons. As mentioned earlier, some limit problems cannot be solved algebraically.
However, you can also use a calculator to check the solution you’ve worked out on pen and paper. Making a table by hand and cross-checking your answer is a great way to understand how a function behaves when close to the arrow number.
Doing this will give you a numerical grasp of the problem, hence enhancing your algebraic understanding of the limit of the function.
Looking at the graph will provide you with further context and improve your grasp of how limits work in calculus.
But using the calculator to work out limits of functions also has some limitations.
You cannot rely on the results you get from the calculator too much. This is because the calculator will only give you an approximate answer – unless you recognize the number the function is getting close to.
For instance, 9.999998 is close enough to 10, and 0.333333332 is close to 1/3.
However, if the limit of the function is a value like 
, you won’t recognize the number if the calculator gives it to you in decimal form. is equal to 0.288675, which is very difficult to recognize.
That said, having access to the answer in decimal form can still help.
The second limitation of using calculators to work out limits of functions is that the calculator cannot work out some functions.
For instance, take the function:
Entering this into a calculator typically fetches no result, while the limit of the function is zero. If you enter a similar function, you won’t get an answer from a calculator.
Meta-Calculator Limit Calculator
If you don’t have a scientific calculator at hand, you can use the Meta-Calculator limit calculator to work out the limits of functions.
As long as you have an internet connection, you can access the calculator through any browser free of cost. It supports finding a limit as x any number – including infinity.
The calculator is easy to use and gives you a result instantly. Meta-Calculator also offers a graphing tool, so getting a visual understanding of a function is as simple as entering the function in the tool.
To find the limit of any function using the Meta-Calculator Limit Calculator:
- Navigate to the Meta-Calculator Limit Calculator from the browser of your choice. The calculator looks like this:
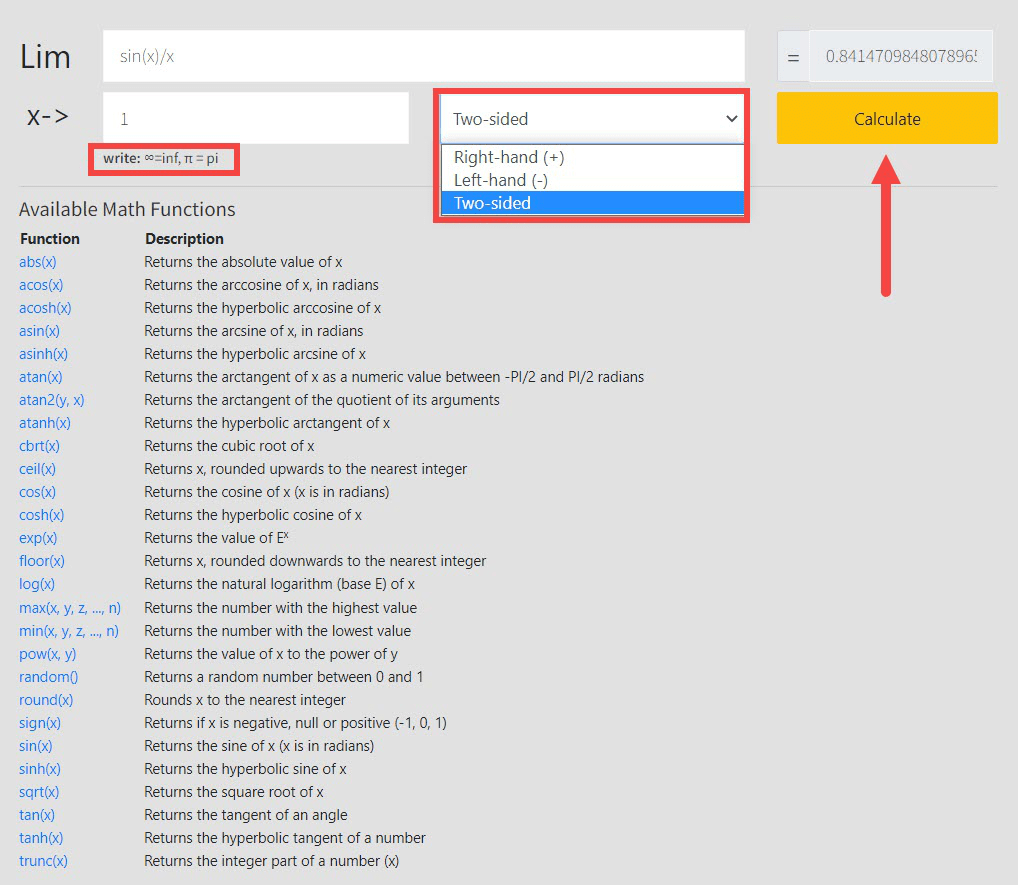
- Enter the function that you want to calculate the limit of in the input box.
- Enter the arrow number in the designated box.
- Select whether you want a two-sided calculation, or just from the right or the left hand.
- Click “Calculate.” Meta-Calculator will work out the limit of the function.
- To calculate the limit of another function, clear the input boxes and repeat from step 2.
Meta-Calculator offers several functions. In addition to trigonometric functions, you can work with hyperbolic functions, arc functions, logarithms, and square roots.
Functions such as abs(x) and floor(x) are also available. With these, you can feed any function you need to find the limit for with ease on Meta-Calculator.
How Does Meta-Calculator Limit Calculator Work?
There are many different ways to evaluate the limits of functions. Some of the methods that the Meta-Calculator Limit Calculator uses are listed below:
- Direct substitution: The first technique that is applied to evaluate the limit of a function is the direct substitution method. Putting the arrow value in most polynomial functions typically solves it. For this reason, most students are instructed to apply this method first. If it fails, then it’s time to consider other methods of evaluating the limit.
- Factorization: There is a chance that on direct substitution, the function will return an indeterminate or undefined form (for instance, 0/0). When this happens, another procedure is required to work out the limit of the function. Factorization is the next go-to method. The numerator and denominator are broken down into their common factors, and when the factors cancel out, the function is reduced to its determinate form. Now that the expression is in its determinate form, the substitution method can be used to work out the limit of the function.
- Rationalization: This is another method used if the function is indeterminate on substitution. Rationalization reduces the function in question to its determinate form, and then the values can be substituted to get the answer.
The Takeaway
It’s recommended that you only use the calculator to verify the answers that you’ve worked out.
Using a scientific calculator to work out the limit of a function can take some work, and depending on the method you choose, there may be many steps involved.
This makes going through the steps doubly taxing when you’re only trying to verify your answer.
But regardless of why you want to work out the limit of a function with a calculator, using the Meta-Calculator Limit Calculator will save you time and effort.
All you have to do is navigate to the site, enter the expression, and select how you want your answer worked out.
Hitting “Calculate” will make the limit of the function appear in a matter of seconds. You can use the calculator from your phone, a tablet, or a computer as long as it has an internet connection.