Top Mathematics Formulas
Here you will find the most common math equations and formulas used in high school and fundamental university courses. These include, but are not limited to, area and volume formulas, the quadratic formula, equations of a line, and trigonometry.
Area, Volume, and Perimeter
Rectangle
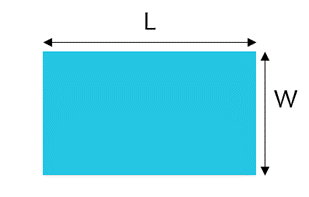
Area of a Rectangle
The area of a rectangle is calculated by multiplying the length (L) by the width (W).
| A = LW |
Perimeter of a Rectangle
The perimeter of a rectangle is the sum of the sides. As the left and right sides are the same width, and the top and bottom are the same length, we can say:
| P = 2L + 2W |
Triangle
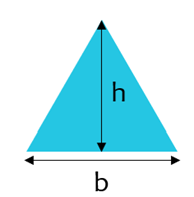
Area of a Triangle
The area of a triangle is calculated by multiplying the base (b) by the height (h) and dividing by 2.
| A = |
|
bh |
Perimeter of a Triangle
The perimeter of a triangle is the sum of each of the sides. In the case of an equilateral triangle, P=3b.
| P = sum of sides |
Circle
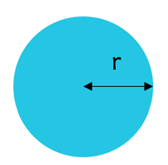
Area of a Circle
The area of a circle is given by pi multiplied by the radius,squared. The radius is half of the diameter of the circle.
| A = πr 2 = |
|
Diameter of a Circle
The length from one end of the circle to the other with a straight line.
| d = 2r = P/π |
Circumference
The circumference of a circle can be thought of as the “perimeter of a circle”. It is calculated by multiplying 2*pi by the radius of the circle.
| P = 2πr = πd |
Rectangular Solid
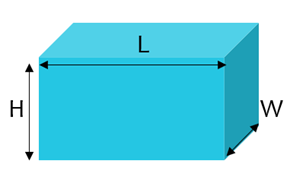
Volume of Rectangular Solid
The volume of a rectangular solid is found by multiplying the length (L), width (W), and height (H).
| V = LWH |
Cone
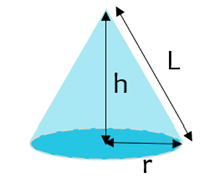
Volume of Cone
The volume of a cone is found by multiplying the area of the base by the height and dividing by 3.
| V = |
|
Sphere
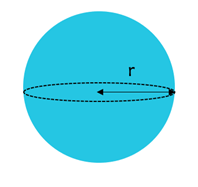
Volume of Sphere
The volume of a sphere is calculated by multiplying (4/3) by pi and the radius, cubed.
| V = |
|
πr 3 |
Quadratic Formula
Solving for x Using the Quadratic Formula
In the quadratic equation in the form shown to the left (second order polynomial), x can be found by using the quadratic formula.
| x = |
|
when ax2 + bx + c = 0
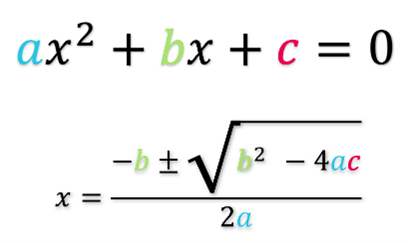
Lines
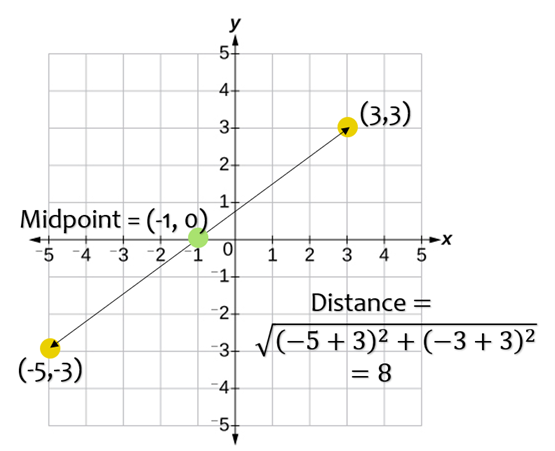
Where the coordinates of Point 1 are given as (x1,y1) and the coordinates of point 2 are (x2,y2)
Distance Between 2 Points
When given the x and y coordinates of 2 points, the distance can be calculated with the formula below.
| d = √(x2 - x1)2 | + (y2 - y1)2 |
Midpoint of 2 Points
The midpoint is the point half way between two given points. When given the x and y coordinates of 2 points, the midpoint can be calculated with the formula below.
| Midpoint = ( |
|
, |
|
) |
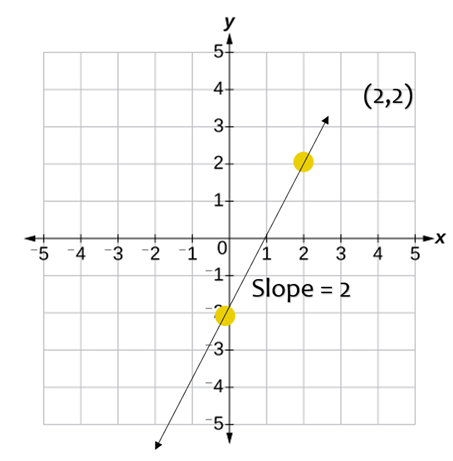
Slope of a Line
The slope of a line is the change in “y” compared to the change in “x”. Colloquially, it is known as “rise over run”.
| Slope = m = ( |
|
) |
Equations of a Line
Slope Intercept Form
The equation of your line can be written in slope intercept form if you know the slope of your line (m) and the y intercept (b).
y = mx + b
Ex. y = 2x - 2
Point Slope Form
The equation of your line can be written in slope intercept form if you know the slope of your line (m) and a point (x1,y1)
y - y1 = m(x - x1)
Ex. y - 2 = 2(x - 2)
Trigonometry
The sine of an angle is calculated by taking the length of the opposite side divided by the length of the hypotenuse.
| sin θ = |
|
The cosine of an angle is calculated by taking the length of the adjacent side divided by the length of the hypotenuse.
| cos θ = |
|
The tangent of an angle is calculated by taking the length of the adjacent side divided by the length of the adjacent side.
| tan θ = |
|
